引用本文
孙丽梅, 许立侠, 徐红梅. 基于Micro-CT初步分析沟裂结构对下颌第一磨牙应力分布的研究[J]. 武警医学, 2016,27(10): 1009-1011
SUN Limei, XU Lixia, XU Hongmei. Influence of fissures on the mandibular first molar based on digital images by Micro-CT[J]. Medical Journal of the Chinese People's Armed Police Forces, 2016,27(10): 1009-1011  

Permissions
Copyright©2016, 《武警医学》编辑部
基于Micro-CT初步分析沟裂结构对下颌第一磨牙应力分布的研究
孙丽梅, 许立侠, 徐红梅
100039 北京,武警总医院口腔科
通讯作者：徐红梅,E-mail:h-m-xu@163.com

作者简介:孙丽梅 ,硕士研究生。

基金资助: 武警总医院院内资助项目(WZ201024)
摘要

目的 探讨沟裂结构对应力分布的影响。方法 建立包含沟裂的下颌第一磨牙有限元模型。采用Micro-CT扫描及ANSYS软件建立包含及不包含牙合面沟裂的下颌第一磨牙有限元模型,并加载500 N载荷,对比两模型应力分布情况。结果 两模型中,拉应力峰值均出现在中央窝沟处,实验组中拉应力峰值为92.48 MPa,对照组为71.34 MPa,实验组拉应力峰值及沟裂处拉应力范围均大于对照组。结论 通过对下颌第一磨牙有限元模型进行力的初步加载,发现牙合面沟裂结构的存在影响力在下颌第一磨牙的分布,对进一步研究隐裂牙受力情况研究提供了基础。

关键词: 下颌第一磨牙; 沟裂; 三维有限元; 应力分布
中图分类号:R781.2
Influence of fissures on the mandibular first molar based on digital images by Micro-CT
SUN Limei, XU Lixia, XU Hongmei
Department of Stomatology,General Hospital of Chinese People’s Armed Police Forces, Beijing 100039,China
Abstract

Objective To investigate the effect of grooves and fissures on stress distribution of the right mandibular first molar.Methods An intact first mandibular molar was scanned with Micro-CT, before ANSYS14.0 software was used to establish a three-dimensional finite element model of the right first molar with or without grooves. 500N was loaded to compare the stress distribution in the two models.Results n the two models, the tensile stress appeared in the fovea groove. The peak tensile stress was 92.48 MPa in the experimental group and 71.34 MPa in the control .The stress peak value and distribution of tensile stress in the experimental group were significantly greater than those in the control group.Conclusion After loading on the two models, it is found that the existence of the grooves structure affects the stress distribution of the mandibular first molar, which requires further research.

Keyword: mandibular first molar; groove; three-dimensional finite element; stress distribution

下颌第一磨牙在发育过程中多个生长叶相连, 在牙冠表面形成近中沟、远中沟等五条发育沟。另外在牙冠上还有副沟、裂、点隙、窝等凹陷部位。在以往关于下颌第一磨牙受力分析的研究中[1, 2, 3], 由于扫描技术等原因, 所建立的有限元模型中不包含内部点隙、沟裂等结构, 对应力在牙表面的分布情况造成一定影响。本研究采用分辨率较高的Micro-CT扫描, 并选择较多扫描图片, 建立包含沟裂结构的下颌第一磨牙有限元模型, 并初步加载载荷, 分析沟裂结构的存在对下颌第一磨牙表面应力分布的影响。

1 材料与方法
1.1材料

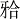
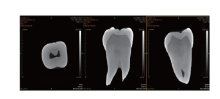
根据中国人下颌第一磨牙的正常值标准, 选择一颗因牙周病拔除的无龋, 无表面裂纹, 咬 面窝沟完整的右下颌第一磨牙(患者, 女, 48岁)。

1.2 方法

(1)将该下颌第一磨牙标本垂直放入塑料泡沫中固定, 放入Micro-CT样品杯中, 使牙长轴与样品杯长轴一致。以14 μ m的扫描分辨率在80 kv 及 500 mA的条件下对样本进行360 ° 旋转扫描。经COBRA软件重建后获得1248张样本的2-D纵断面图像, 并以Dicom的格式输出(图1)。(2)下颌第一磨牙有限元模型的建立。从获得的1248张Dicom图像每隔3张选取1张, 将获得的312张图片转换成Mmics格式, 构建包含及不包含沟裂结构的下颌第一磨牙有限元模型(图2、3)。(3)材料参数对各物质定义, 并将沟裂内物质弹性模量分别定义为0 及83000 MPa, 构建包含及不包含沟裂的有限元模型, 即本实验的实验组及对照组(表1)。(4)实验条件假设。实验过程中将釉质、牙本质等各种组织材料均视为连续、各向同性的均质弹性材料[4, 5, 6]。(5)边界条件。本实验中, 该牙的颊舌侧以及底部牙槽骨完全固定约束, 其余各面均为自由边界[2]。(6)加载条件。在磨牙面中央窝沟处置一直径为2 mm的小球, 于小球上端垂直加载500 N的力, 模拟正中咀嚼时磨牙受力情况。

图1 Micro-CT扫描后某断面

图2 下颌第一磨牙有限元模型

图3. 右下颌第一磨牙各组织有限元模型

表1 下颌第一磨牙有限元模型的材料参数
1.3观察指标

本实验主要观察牙体表面拉应力(S1)的分布情况, 应力值前有“ -” 表示压应力, 无“ -” 表示拉应力。在应力云纹图上, 以由蓝至红各颜色表示应力分布情况, 越接近红色表示拉应力值越大, 越接近蓝色表示压应力值越大。

2 结果

载荷加载后, 两模型应力峰值主要分布在力的直接接触区域, 即与小球接触的颊舌尖的牙尖斜面处。在咬 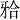面其他位置, 两模型除直接接触区有压应力集中外, 其他部位可见压应力均匀分布。拉应力主要集中在中央窝沟处, 且实验组中拉应力在近远中沟裂处分布范围广。实验组中拉应力峰值为92.48 MPa, 对照组中拉应力峰值为71.34 MPa。力在两模型中的分布情况如图4。

图4 加载后实验组与对照组拉应力分布^A.实验组, B.对照组

3 讨论

有限元分析方法是解决生物力学问题, 尤其是复杂力学问题时的一种快捷有效的工具。采用有限元分析方法进行应力分析最关键的步骤就是高效快捷地建立精确的有限元模型[8, 9, 10]。三维有限元模型的建立方法较多:一种是磨片、切片法, 将牙使用环氧树脂等材料进行包埋后切片获得各截面信息; 另一种是采用各种测量仪器对牙齿进行扫描, 获取所需的截面信息。二维截面信息的获取是一个复杂的过程且具有较大的主观性, 而模型与标本的相似程度是由各个二维截面信息决定的。

目前, 较常采用的获取二维信息的方法主要包括螺旋CT、CBCT等技术。Kim I等[10]回顾分析了计算机三维技术在牙体结构重建中的作用后提出, 原始数据的精确度和丰富性是建立牙齿三维结构数据库的基础和前提。随着技术的发展, Micro-CT扫描技术出现, 并逐渐应用于有限元分析中。该方法具有较高的精确性, 分辨率以及无创性等优点。本实验中, 采用Micro-CT以14 μ m层间距扫描, 所获得的二维信息精确度高, 图片中包含各沟裂的内部沟裂结构; 另外, 在建立三维模型过程中每隔3张选取一张二维图片, 各断层间距离较小, 这就为本实验建立包含沟裂结构的精确地磨牙有限元模型提供了基础和前提条件。

釉质是一种抗压不抗拉的牙体硬组织。在本实验研究中, 主要关注加载应力后两模型拉应力分布的差异。同等载荷加载后, 两模型的应力分布存在明显差异:实验组中, 拉应力峰值明显大于对照组, 拉应力主要分布在 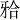面中央窝沟、近远中窝沟等处; 对照组中, 仅在中央窝沟处见较大面积的拉应力分布区, 且拉应力值小于实验组。合力加载后, 磨牙窝沟等处出现拉应力集中的现象与以往研究相一致[12, 13]。两模型的差异主要在于沟裂处物质弹性模量的设定, 可能是由于对照组中沟裂内部物质弹性模量较大, 对力的传导起到了一定的阻碍作用, 使窝沟处拉应力值低于实验组。该结论与Benazzi S等[14]关于类人猿下颌磨牙的应力分布结果相一致。

面窝沟等结构的形成过程较为复杂, 下颌第一磨牙由5个生长叶发育形成, 发育沟的形成有其特点[15, 16]。首先, 相邻近的2个生长中心相互融合, 由于各生长叶生长中心尖端的生长发育速度较快, 在生长叶之间逐渐形成生长中心尖端至边缘处的斜坡。该生长中心处继续生长发育, 并逐渐形成牙釉质, 在各个牙尖的高起部位, 可以观察到, 相互融合的2个生长中心之间的斜坡逐渐变得更为高陡。随着下颌第一磨牙牙釉质的进一步形成, 成釉细胞由斜坡表面处逐渐后移, 由于斜坡相邻的两侧成釉细胞层的基底层部位相互接触, 导致该处釉质形成受阻, 最终使该处成为牙釉质生长发育较为薄弱的部位; 相邻的牙尖斜面并不是平坦的, 斜面内部的转折部位基底膜接触较其他部位早, 造成该处牙釉质生长发育的时间明显减少, 最终导致两牙尖相邻的牙尖斜面内部牙釉质的厚度减少, 当牙釉质发育形成后, 在该部位沟裂处形成一种独特的结构, 即沟裂中心分布有成釉细胞形成的独特的条索状结构, 两侧为薄弱的牙釉质; 磨牙萌出后, 这种特殊的条索状结构逐渐退化、分解, 该结构所占据的空间逐渐显露出来, 成为周围有薄弱牙釉质包绕的沟裂结构, 成为牙体发育过程中的薄弱环节。而加载合力后, 该处又有拉应力的集中, 由于釉质是一种抗拉能力较差的牙体硬组织, 易造成牙隐裂等应力疲劳性疾病的发生。

综上所述, 本实验通过对包含内部沟裂结构的下颌第一磨牙进行力的初步加载, 发现窝沟处有拉应力的集中, 且拉应力值较大, 从力学分析的角度解释了临床中常见的牙隐裂等现象。该研究模型的设计也为进一步分析沟裂结构对牙体应力分布的影响奠定了理论基础。

The authors have declared that no competing interests exist.

参考文献
[1] Amaral M T, Guedes-Pinto A C, Chevitarese O C. Effects of a glass -ionomer cement on the remineralization of occlusal caries-an in situ study[J]. Braz Oral Res, 2006, 20(2): 91-96. [本文引用:1]
[2] Srirekha A, Bashetty K. Infinite to finite: an overview of finite element analysis[J]. Indian J Dent Res, 2010, 21(3): 425-432. [本文引用:2]
[3] 曾艳, 王嘉德. 下颌第一恒磨牙三维有限元模型的建立及应力分析[J]. 中华口腔医学杂志, 2009, 40(5): 394-397. [本文引用:1]
[4] Rodrigues F P, Li J, Silikas N. Sequential software processing of micro-XCT dental-images for 3D-FE analysis[J]. Dent Mater, 2009, 25: 47-55. [本文引用:1]
[5] Lima I N, Barbosa G F, Soares R B, et al. Creating three-dimensional tooth models from tomographic images[J]. Stomatologija, 2008, 10(2): 67-71. [本文引用:1]
[6] 周书敏, 何明元, 张延宏, 等. 牙根尖区应力分布的三维有限元计算[J]. 北京大学医学学报, 1988, 20: 31-35. [本文引用:1]
[7] 符红梅, 贾静, 朱晓英, 等. 根管治疗后下颌磨牙采用各种充填材料修复的三维有限元分析[J]. 口腔颌面修复学杂志, 2014, 15(2): 75-79. [本文引用:1]
[8] Takada H, Abe S, Tamatsu Y, et al. Three- dimensional bone microstructures of the mand ibular angle using micro- CT and finite element analysis: relationship between partially impacted mand ibular third molars and angle fractures[J]. Dent Traumatol, 2006, 22(1): 18-24. [本文引用:1]
[9] Dejak B, Mlotkowski A, Romanowicz M. Finite element analysis of mechanism of cervical formation in simulated molars during mastication and paratunction[J]. J Prosthet Dent, 2005, 94: 520-529. [本文引用:1]
[10] Cuy J L, Mann A B, Livi K J, et al. Nanoindentation mapping of the mechanical properties of human molar tooth enamel[J] . Archives of Oral Biology, 2002, 47: 281-291. [本文引用:2]
[11] Kim I, Paik K S, Lee S P. Quantitative evaluation of the accuracy of micro-computed tomography in tooth measurement[J]. Clin Anat, 2007, 20(1): 27-34. [12] Benazzi S, Kullmer O. Using occlusal wear information and finite element analysis to investigate stress distributions in human molars[J]. J of Anat , 2011, 219: 259-272. [本文引用:1]
[13] Magne P, Belser U C . Rationalization of shape and related stressdistribution in posterior teeth: a finite element study using nonlinear contact analysis[J]. Int J Periodontics Restorative Dent, 2002, 22: 425-433. [本文引用:1]
[14] Benazzi S, Kullmer O, Grosse I R, et al. Unravelling the functional biomechanics of dental features and tooth wear[J]. Plos One, 2013, 8(7): 1-10. [本文引用:1]
[15] Finke M, Hughes J A, Parker D M, et al. Mechanical properties of in situ demineralised human enamel measured by AFM nanoindentation[J]. Surface Science, 2001, 491: 456-467. [本文引用:1]
[16] Ge J, Cui F Z, Wang X M, et al. Property variations in the prism and the organic sheath within enamel by nanoindentation[J]. Biomaterials. 2005, 26(16): 3333-3339. [本文引用:1]